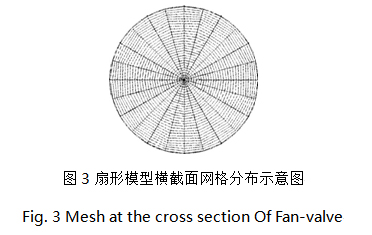
调节阀作为流量控制系统中的重要元件,通过改变其自身阻力特性调节系统的介质流量,其调节质量影响到整个系统的效率和稳定性。依照系统的调节需要设计调节阀,关键是设计调节阀结构及其阀芯的流通面积分布。
目前已有的关于调节阀流量特性的研究主要集中在以下几个方面,一是流量调节理论的研究,包括数学模型的建立和完善、评价标准的讨论等。二是针对具体阀型,利用试验或工程经验,分析流量特性和改进方法;三是针对具体阀型,利用CED技术分析流量特性-。。对于流量特性与流通面积分布两者之间联系的讨论,文献中阐述了借助实验数据和流体阻力系数一流通面积間线图,或利用总流量系数等参数,计算特定形式调节阀的流通面积分布的方法;文献[ 8」中也针对具体调节阀,提出了通过调整面积一行程分布改善流量特性的方案,并与实验结果进行了比较。然而这些研究都是针对具体形式的调节阀,且依赖经验数据和实验数据,其意义在于具体工程应用,并没有在理论层面分析流量特性与流通面积分布之间的联系。而网孔型套筒阀的流量特性,也没有相关文献对其进行分析。
本文设计了两种不同结构的简化模型,对其进行数值模拟研究,旨在分析其流量特性与流通面积分布关系之间的联系,从中寻找规律。在此基础上,对一种网孔型套筒阀进行了优化,计算了优化前后两种调节阀的流量特性,并进行了比较分析。
调节阀的流量特性是指通过调节阀的流体的相对流量与相对开度之间的关系,包括理想流量特性和工作流量特性。
流量控制系统由调节阀和其他系统元件共同构成,系统流量取决于系统的总阻力。因此,在不同的系统中,即使是相同的调节阀、相同的开度,流量也并不相同。而调节阀的理想流量特性能够反映调节阀自身的调节特性:即调节阀前后压差恒定的情况下,相对流量与相对开度之间的关系为调节阀理想流量特性(也称调节阀的固有特性),其关系曲线称为理想流量特性曲线,用数学表达式(l)表示。
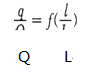
式中:q/Q为相对流量;//L为相对开度。
在常见的调节阀中,有四种典型的流量特性曲线,即直线型、对数型(也称等百分比型)、快开型、抛物线型」,分别对应图1中的曲线1、2、3、4。直线型流量特性的调节阀,流量随行程线性变化,在小开度时流量变化明显(流量变化量与流量的比值大),调节灵敏度高,而在大开度时,流量变化相对缓慢(流量变化量与流量的比值小),调节灵敏度低,因而出现大开度下调节能力不足等问题,因此在一些情况下不能满足调节要求。对数型流量特性的调节阀,流量变化速度逐渐加快,小开度时流量变化缓慢,调节精度高,大开度时流量变化相对较快,能保持良好的调节能力,这些特点使其在工程中得到了广泛的应用。抛物线型调节阀的调节特性介于直线型和对数型两者之间田,这种特性的调节阀在工程应用中也比较常见。快开型调节阀的调节特点与对数型相反,小开度时流量迅速变化,达到快速加大流量的目的,而大开度时流量变化缓慢。除了这四种典型曲线外,还有双曲线型、平方根型等流量特性曲线,但并不常见。
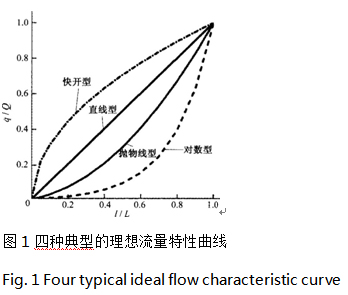
事实上,具体到实际的调节阀时,其理想流量特性曲线很难与四种典型的理想流量特性曲线完全重合,往往是近似某种形式,如普通蝶阀的理想流量特性通常介于直线型和对数型曲线之间。选择和设计调节阀时,须根据具体要求选择适当的流量特性曲线作为设计参考。
对于某些结构形式的调节阀,根据经验公式或实验参数,可以得到其理想流量特性曲线与流通面积分布之间的关系,据此可以由选定的理想流量特性曲线计算调节阀的流通面积分布。针对几种具体结构形式的调节阀,文献[ 0中介绍了计算流通面积分布的方法,但都需要实验或经验参数作为条件,并不适用于其他结构的调节阀。
安装在调节系统中的调节阀,随着管路阻力等工作条件的变化,调节阀的前后压差不再保持恒定,此时调节阀的相对流量与相对行程之间的关系称为调节阀的工作流量特性。用数学表达式表示为:
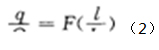
Q L 式中符号意义同公式(1)。 理想流量特性曲线和工作流量特性曲线可以通过公式(3)建立联系「2」。
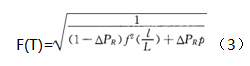
式中PR为压降比,表示调节阀前后压差占调节系统总压降的比值。
文献[ 7 ]中阐述了选取压降比APR的方法,若压降比选定,则可依照公式(3)岫系统需求的工作流量特性曲线推导出对应的理想流量特性曲线,若理想流量特性曲线与流通面积分布的关系已知,便可推求调节阀的流通面积分布。
本文设计了两种调节阀的简化模型,根据其流通截面的形状,分别称之为扇形模型和环形模型,其流通截面的结构如图2 所示。扇形模型的流通截面为扇形,设定其在0、360。范围内随行程均匀变化,流通面积与行程的关系为线性。环形模型的流通截面为圆形,设定其直径随行程均匀变化,易知其流通面积与行程的关系为平方关系。需要说明的是,此两种模型并不能直接适用工程应用,本文用来计算,旨在理论研究。
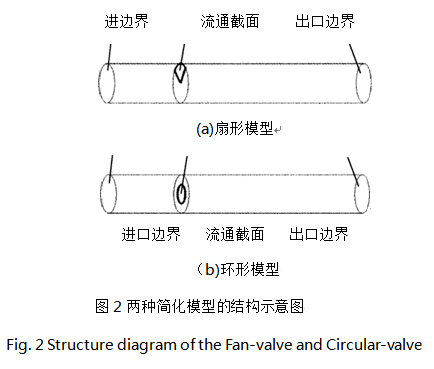
本文的数值模拟研究基于PROE软件建模,GAMBIT软件划分网格、FLUENT软件求解。按图2中所示的结构建立模型:管路直径] 200 mm,管道长度取阀前2,100 mm,阀后 20 000 mm(初步计算取5倍直径时出口有回流),分别建立调节阀在不同开度下的模型。网格划分:采用非结构网格划分,扇形模型总网格数量为13万个左右,环形模型为10万个左右,扇形模型垂直于轴向的横截面上网格形状如图3,网格沿轴向均匀分布,环形模型类似。求解计算:设置定常流动,选用标准湍流模型,设置流体介质为水一1 kg/L),进出口压差为105 Pa(进口总压105 Pa,出口表压0 (a)o通过计算不同开度下的流量,拟合出模型的理想流量特性曲线,如图4。