【续】调节阀流量特性分析及网孔型套筒阀优化计算

结果分析

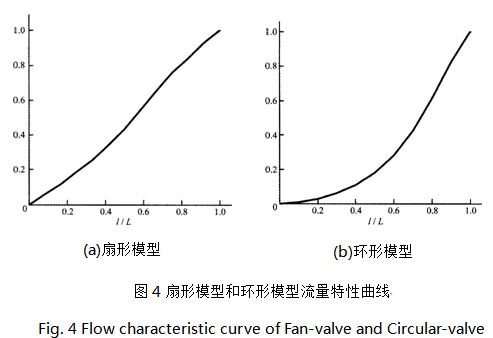
由图4（a）曲线可以发现，扇形阀的相对开度在0、0 • 7范围内时，流量曲线略微下凹，表明这一行程范围内流量变化速度先慢后快；而相对开度在0 • 7、1区间内时，几乎与直线型重合，说明大开度下扇形模型具有直线型流量特性，流量线性变化。结果表明，扇形模型的流量特性曲线介于直线型和对数型之间，且十分接近直线型曲线。

由图4（b）曲线可以发现，随着开度的增加，曲线斜率逐渐增大。大致可分为3个区域：相对开度在0、0.4的区域附近时，曲线斜率小于1，流量变化速度缓慢；相对开度在0. 4、0 .5 的区域附近时，曲线斜率接近1，流量均匀变化；相对开度在0.5 、1时，曲线斜率大于1且迅速增大，流量变化速度加快。结果表明，环形模型的理想流量特性曲线接近对数型。

将两种简化模型的流量特性曲线进行对比，容易发现两种不同结构的模型对应不同的流量特性：扇形模型的流通面积与行程之间是线性关系，其理想流量特性曲线接近直线型；而环形模型的流通面积与行程之间是平方关系，其理想流量特性曲线接近对数型。结果验证了调节阀的流通面积分布是其流量特性的重要影响因素，而且其影响呈现出一定的规律性。

网孔式套筒调节阀流量特性分析

流通面积分布影响调节阀流量特性。根据这一思想，本文对一种网孔型套筒阀进行了优化，仿真i十算了优化前后两种阀的流量特性，对比分析了两者的调节特性。

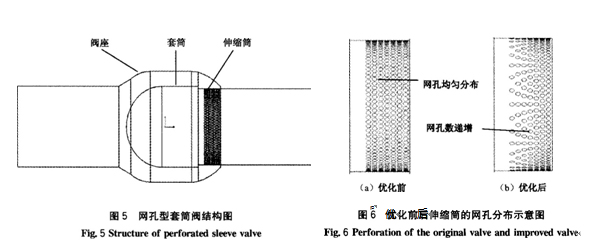
本文选择的网孔型套筒阀结构如图5所示，通过调节伸缩筒的位置来控制流通面积，从而实现流量调节，伸缩筒从右向左运动，依次实现1、7列网孔过流。优化前的网孔，沿环向均匀分布直径为30 mm的圆形孔，每列90个，如图6(a)O而优化方案则通过改变网孔的分布来改变其流量特性，网孔数量从 1、7列依次递增，分别为30、40、50、60、70、80、90个，如图6（b)。

数值计算

管路直径为1 200 mm，管路长度取阀前6 000 mm,阀后12 000 mm；由于模型结构相对复杂，故采用四面体网格与六面体网格相结合的方法进行网格划分，对于网孔附近的区域，因其网孔小、前后压差变化大，故而采取加密处理，总网格数量在 35、50万之间，因加密区域范围不同而异，网格划分结果如图7。分别计算并拟合出两种阀的流量特性曲线，结果如图8。

结果分析

优化前网孔型套筒阀的网孔均匀排列，流通面积随行程线性分布，这一特点与第二节中的扇形模型一致。计算结果表明该型调节阀的流量特性曲线为直线型（如图8中曲线l)，与扇形模型的近似。此阀具有直线型的调节特点，能满足流量线性变化的系统需求。

优化后的调节阀的网孔数量随开度的增加逐渐递增，其流通面积与行程的关系为非线性，且介于线性关系和平方关系之间。计算结果表明其流量特性曲线为抛物线型（如图8中曲线 2），介于直线型和对数型之间，对比第二节中两种简化模型，可以发现流量特性与流通面积分布的关系是相对应的。计算结果同时表明，此阀具有抛物线型流量特性的调节特点，较之优化前，此阀在小开度时流量变化缓慢，大开度时调节灵敏度较高，能满足流量调节要求为抛物线型的系统需求。通过优化，该型网孔型套筒阀实现了更多的流量调节特性。

结语

• 不同流通面积一行程分布关系的调节阀，其流量特性具有各自的特点：扇形模型的流通面积与行程是线性关系，其理想流量特性曲线趋近于直线型；环形模型的流通面积与行程是平方关系，其理想流量特性曲线趋近于对数型（等百分比型）。可以预测，其他流通面积分布的调节阀也有与其相对应的流量.
• 优化前的网孔型套筒阀，网孔均匀分布，流通面积与行程是线性关系，结果表明其流量调节特性为直线型。优化后的调节阀，网孔数量逐渐递增，流通面积与行程是非线性关系，且介于线性关系与平方关系之间，结果表明其流量特性曲线为抛物线形，介于直线型与对数型之间。与扇形和环形两种简化模型对比发现，优化前后两种网孔型套筒阀的流量特性与面积分布的关系符合结论（1)所述的规律，证明了根据结论（1）对调节阀的流量特性进行优化的合理性。
• 通过改变伸缩筒上的网孔分布，优化了网孔型套筒阀的流量特性。可以预测，通过设计其他不同的网孔分布或网孔形状，可以实现其他多种形式的流量特性，从而满足不同的调节要求。